Optimizing Global Injectivity for Constrained Parameterization

Xingyi Du, Danny M. Kaufman, Qingnan Zhou, Shahar Z. Kovalsky, Yajie Yan, Noam Aigerman, Tao Ju

ACM Transactions on Graphics (Proc. SIGGRAPH Asia 2021)

PDF Code Dataset Slides Video DOI PDF (Low Res)

featured — Figure 1. Given a non-injective initial parameterization of a surface mesh (left) with inverted triangles (red), boundary intersections (orange dots), and overwound vertices (magenta dots), our method recovers a globally injective map (right) while keeping the constraints (blue points) in place. The inserts zoom in on one region in the initial map with many boundary intersections and inverted triangles (green box) and another region with an overwound vertex (cyan box).

Abstract

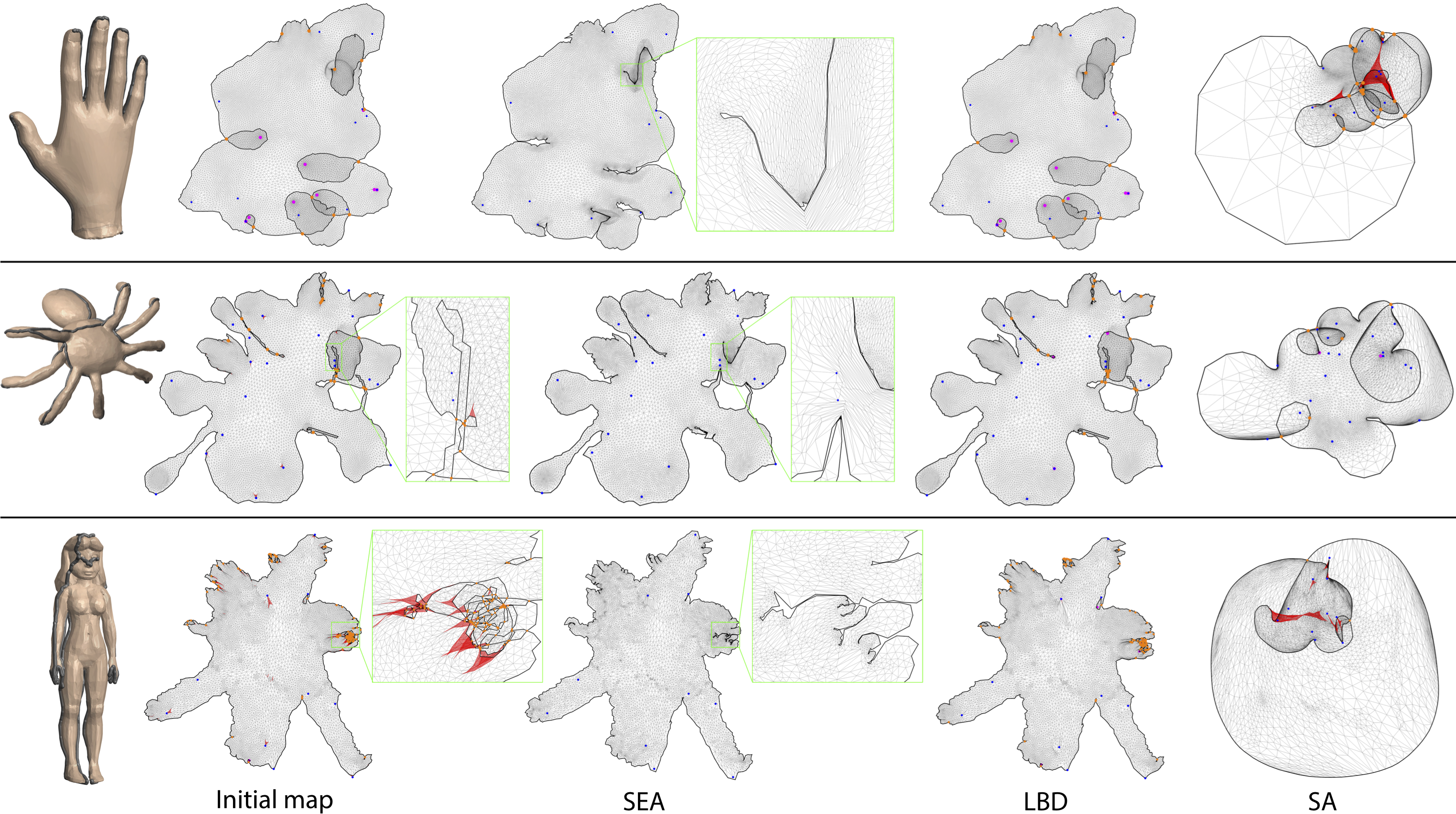
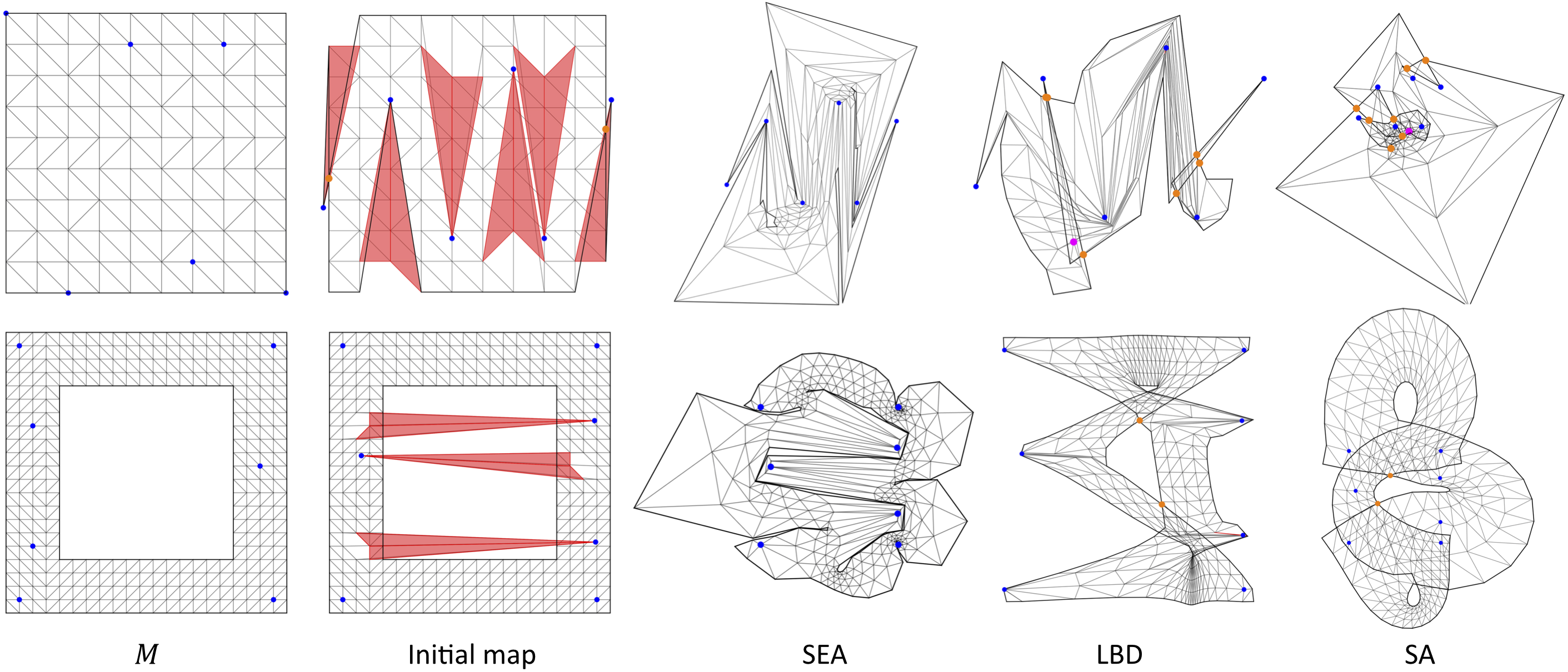
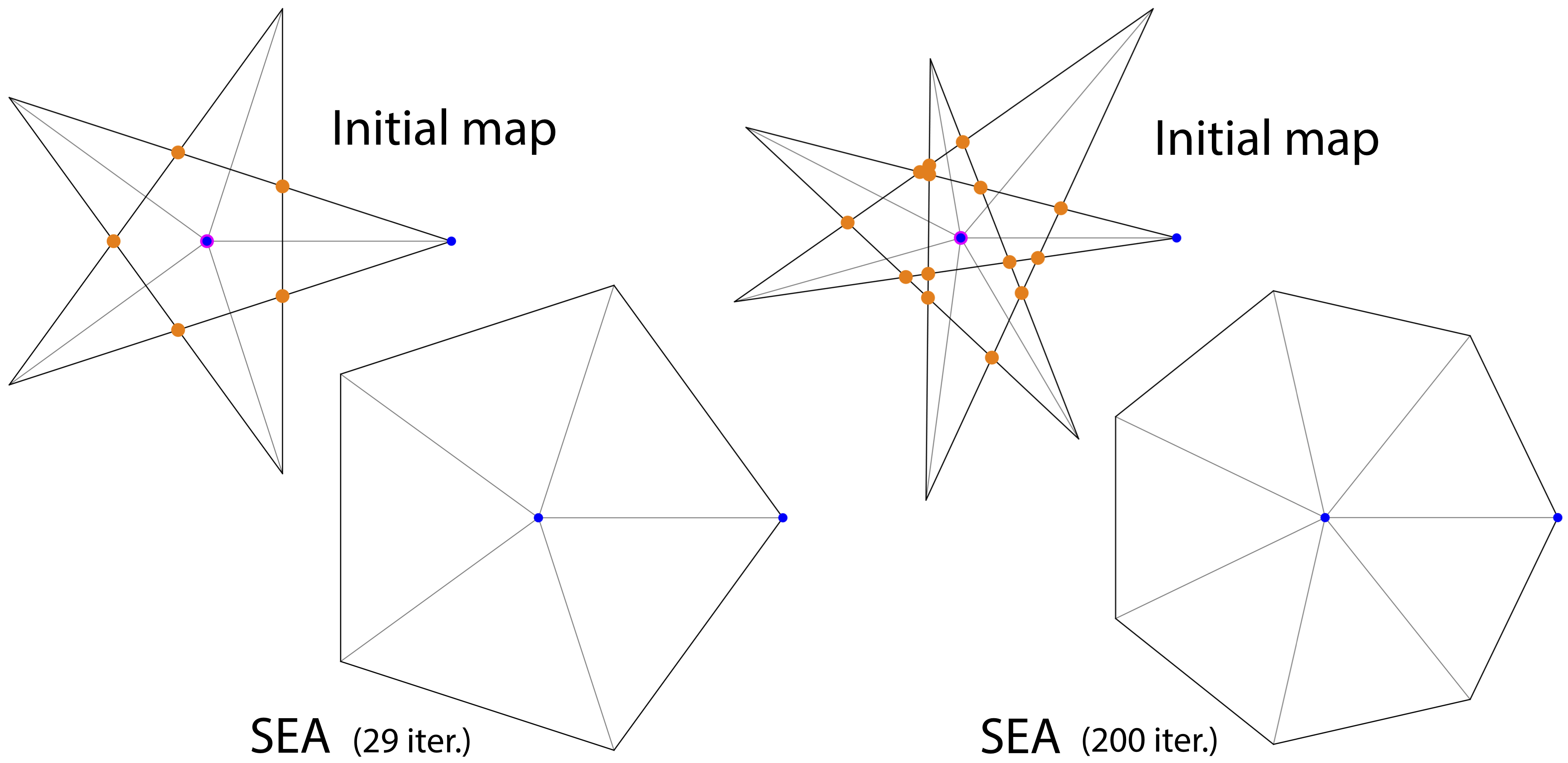
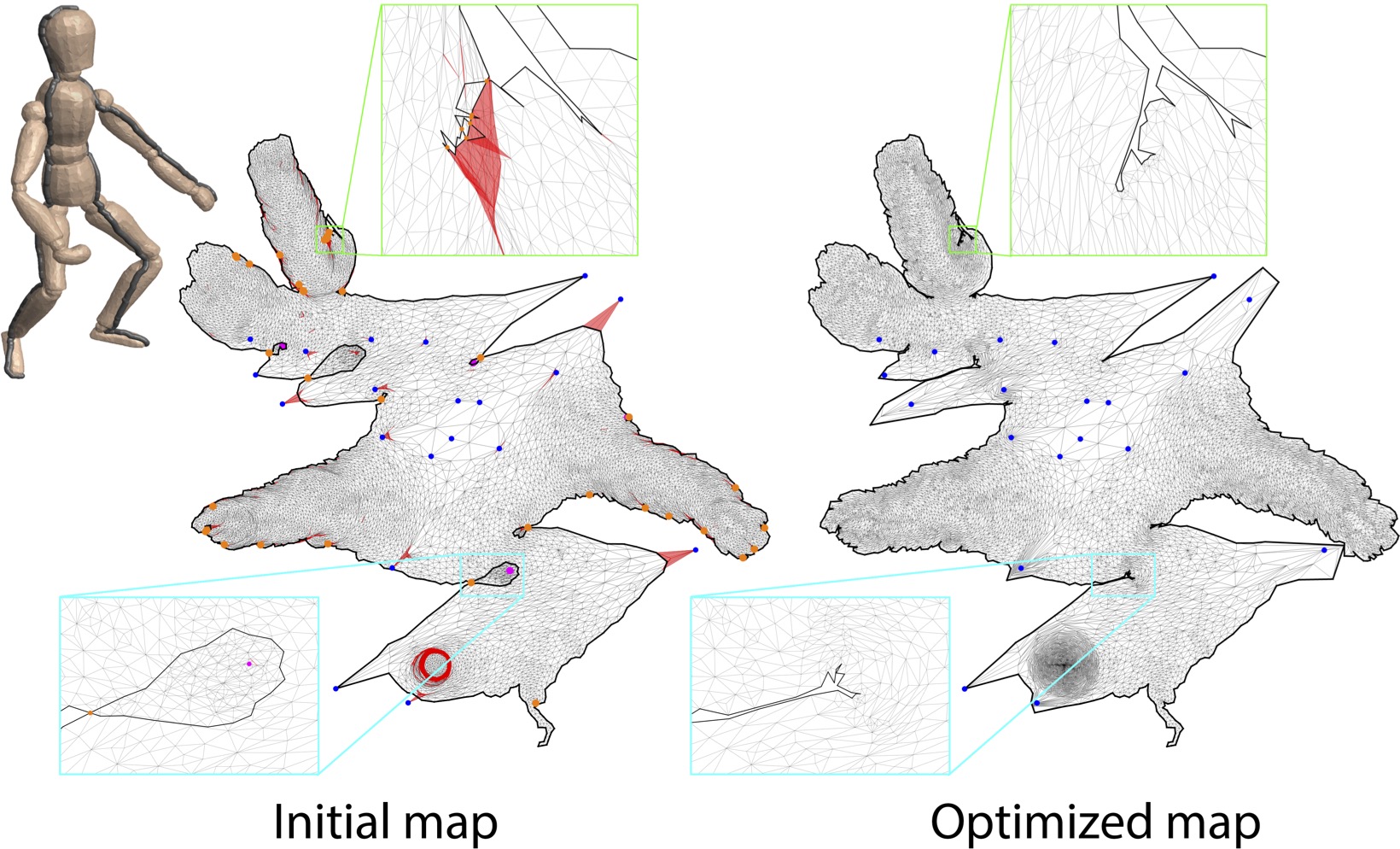
Injective parameterizations of triangulated meshes are critical across applications but remain challenging to compute. Existing algorithms to find injectivity either require initialization from an injective starting state, which is currently only possible without positional constraints, or else can only prevent triangle inversion, which is insufficient to ensure injectivity. Here we present, to our knowledge, the first algorithm for recovering a globally injective parameterization from an arbitrary non-injective initial mesh subject to stationary constraints. These initial meshes can be inverted, wound about interior vertices and/or overlapping. Our algorithm in turn enables globally injective mapping for meshes with arbitrary positional constraints. Our key contribution is a new energy, called smooth excess area (SEA), that measures non-injectivity in a map. This energy is well-defined across both injective and non-injective maps and is smooth almost everywhere, making it readily minimizable using standard gradient-based solvers starting from a non-injective initial state. Importantly, we show that maps minimizing SEA are guaranteed to be locally injective and almost globally injective, in the sense that the overlapping area can be made arbitrarily small. Analyzing SEA’s behavior over a new benchmark set designed to test injective mapping, we find that optimizing SEA successfully recovers globally injective maps for 85% of the benchmark and obtains locally injective maps for 90%. In contrast, state-of-the-art methods for removing triangle inversion obtain locally injective maps for less than 6% of the benchmark, and achieve global injectivity (largely by chance as prior methods are not designed to recover it) on less than 4%.

Video

Fast Forward

Summary

Presentation

Optimization Process

The process of optimizing SEA (smooth excess area) on the examples presented in the paper.

Dataset

We create a benchmark dataset for evaluating various methods’ capability to recover an injective mapping from a non-injective initial mapping while keeping a group of positional constraints in place.

The dataset includes 1791 triangular mesh examples. Each example contains

input.obj: rest mesh and initial mesh (as UV coordinates)
handles.txt: list of indices of the fixed vertices
groundTruth.obj: globally injective mesh satisfying positional constraints

We also provide the result of our method for each example.

Download Dataset

Code

Source code is hosted on github.

Figures

fig-success — Figure 2. Three successful examples from the benchmark: initial maps (first column), maps produced by our method (second column), which are all globally injective, and maps produced by LBD (third column) and SA (last column), none of which are locally or globally injective.

fig-toys — Figure 3. From left to right: input meshes (with one or two boundaries), non-injective initial maps, globally injective maps produced by our method (SEA), and results of LBD and SA. Both LBD and SA have removed most or all inverted triangles, but the results are neither locally or globally injective due to overwound vertices and boundary intersections.

fig-overwound-1-rings — Figure 4. Two initial maps with overwound vertices (top) and the injective maps produced by our method (bottom).