Lifting Simplices to Find Injectivity

Xingyi Du, Noam Aigerman, Qingnan Zhou, Shahar Z. Kovalsky, Yajie Yan, Danny M. Kaufman, Tao Ju
ACM Transactions on Graphics, 2020, Vol.39, No.4 (Proc. SIGGRAPH 2020)
PDF Code Dataset Slides Video DOI PDF (Low Res)
fig1
Figure 1. Injectively mapping a complex surface mesh (Lucy, 48K vertices) to a non-convex boundary (letter “G”, with zoom-ins), on the left, and mapping a tetrahedral mesh (Armadillo, 6K vertices) to a highly deformed target surface, on the right, as a result of minimizing our novel energy. These two examples are part of our new benchmark data set.

Abstract

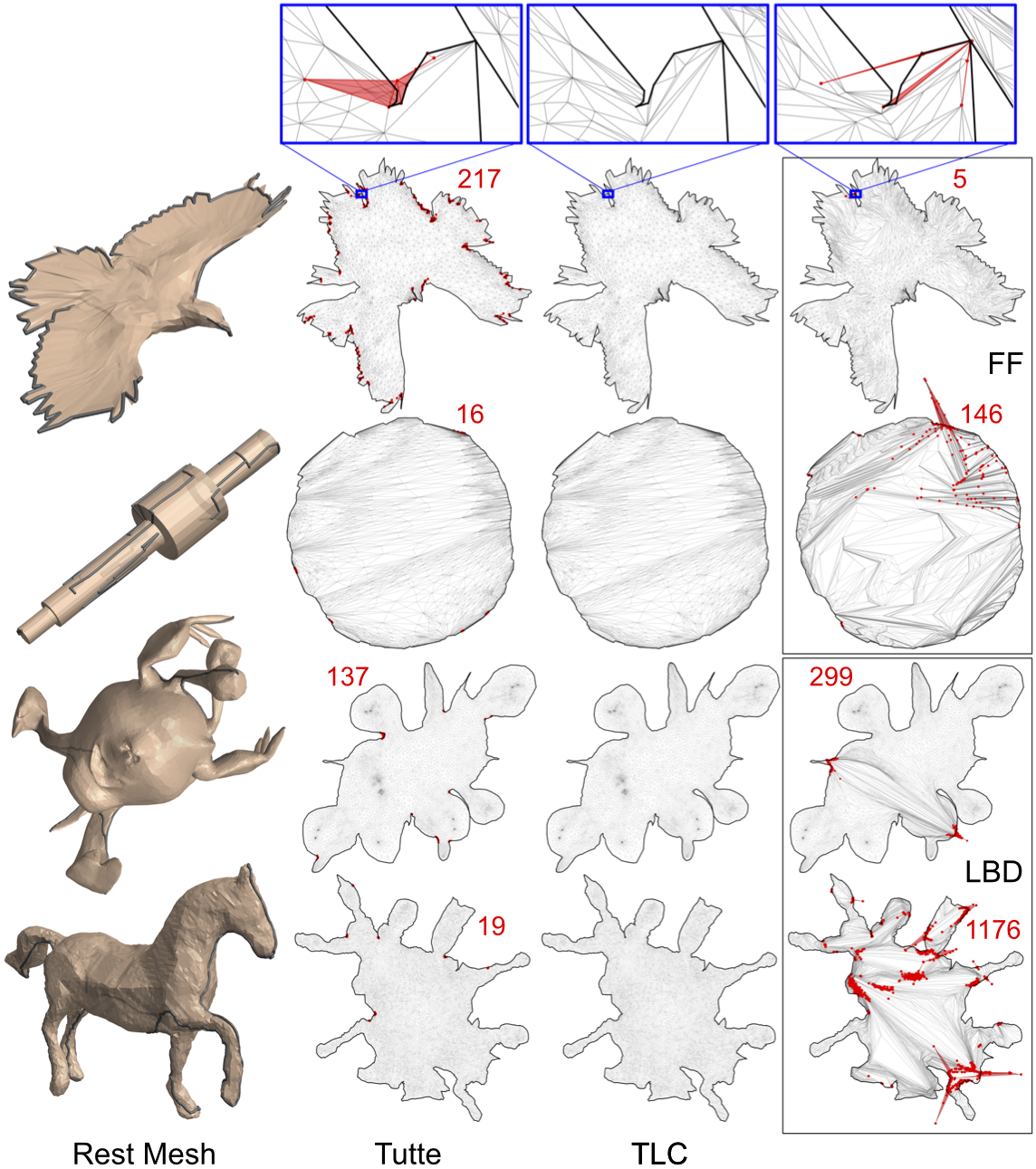
Mapping a source mesh into a target domain while preserving local injectivity is an important but highly non-trivial task. Existing methods either require an already-injective starting configuration, which is often not available, or rely on sophisticated solving schemes. We propose a novel energy form, called Total Lifted Content (TLC), that is equipped with theoretical properties desirable for injectivity optimization. By lifting the simplices of the mesh into a higher dimension and measuring their contents (2D area or 3D volume) there, TLC is smooth over the entire embedding space and its global minima are always injective. The energy is simple to minimize using standard gradient-based solvers. Our method achieved 100% success rate on an extensive benchmark of embedding problems for triangular and tetrahedral meshes, on which existing methods only have varied success.

Video

Dataset

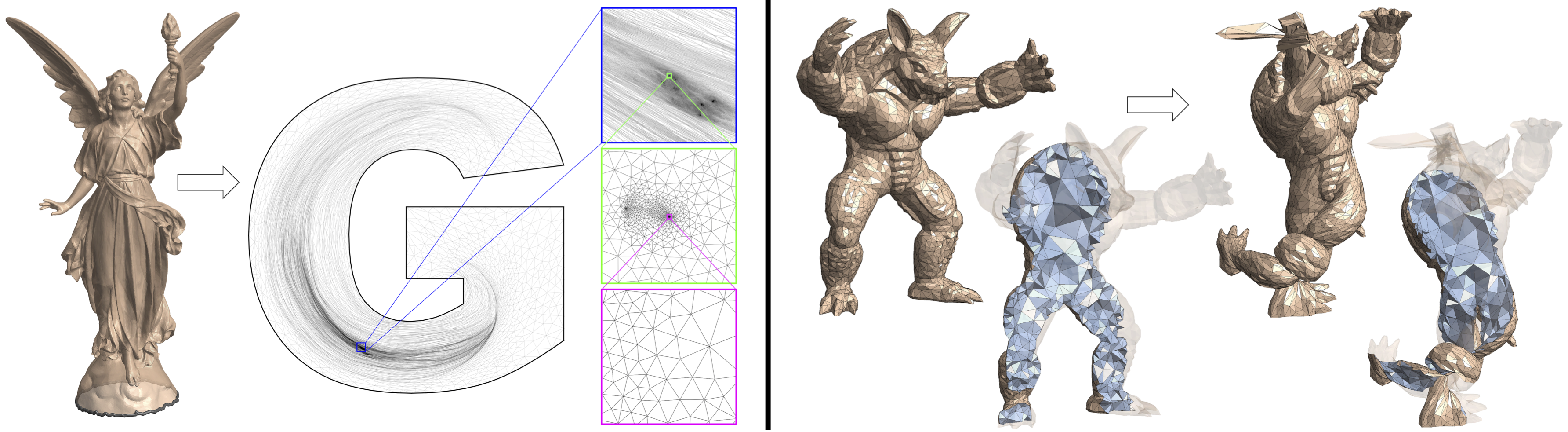
We present the large benchmark dataset of 2D/3D meshes used to compare with previous methods. The dataset includes 10743 triangular mesh examples and 904 tetrahedral mesh examples. The dataset is divided into 3 categories, 2D parameterization, 3D parameterization and 3D deformation.

2D Parameterization

2D Parameterization
Figure 2. Four examples in the 2D parameterization category derived from [Liu et al. 2018], where methods FF and LBD failed to find injective embeddings. Inverted triangles are colored in red, and the numbers of inversion are marked in red.

3D Parameterization

3D Parameterization
Figure 3. Three examples from the 3D parameterization category, each mapping a rest tetrahedral mesh into a sphere (top), smooth surface (middle), and a polycube (bottom). Each example is a failure case for one of the three methods, FF, LBD and SA. Inverted tetrahedra are colored in red, and the numbers of inversion are marked in red.

3D Deformation

3D Deformation
Figure 4. Three examples in the 3D deformation category (a twisting armadillo) where FF, SA and LBD all failed to reach injectivity. The graph in the top-right shows the number of inverted tetrahedra for each of the 600+ frames of the deformation sequence (ellipses indicate the frames from which the three examples were taken).

Dataset Organization

Each triangular mesh example contains

  • input.obj: rest mesh and initial mesh (as uv coordinates)
  • handles.txt: list of indices of the fixed vertices
  • result.obj: result of our method

Each tetrahedral mesh example contains

  • rest.vtk: rest mesh
  • init.vtk: initial mesh
  • handles.txt: list of indices of the fixed vertices
  • result.vtk: result of our method

Here is an introduction to VTK format.

Download Dataset